SPECTRUM OF INTERPRETATION
1. DEVOTIONAL 2. ANALYTICAL 3. CRITICAL 4. HOLISTIC

PRAYER
Oh glorious and amazing God, we praise You. You who have spoken through the ages to your seers and prophets; You who have come in such mysterious and awe-inspiring forms: a burning bush, a whispered voice, a pillar of fire. Your heavenly messages arrived, delivered to the sages through burning wheels, and many-headed Creatures. We forget Your strangeness easily. We shrink from speaking of “the fear of God,” who’d have our sacredness a pleasant thing to smile at and play guitar for. But the history of revelation tells a different tale. Full of sublime otherness. Full of the stuff beyond our ken.
Now you have added this glorious Enigma to your forms:
“My God! He rises! Blooms.
Unfolds. Unfurls in fire. In flame. In wreathes
of burning circles like a helix dance—
and turning. Every movement, sprig and fleck
of pigment, every flourishing of hue
and shape: imperative, all-necessary,
as the great Gear, Being-Becoming, grows,
styles, stigmas, pistils, petals, stamens, anthers
into the air—into epiphany!
and turns the very atmosphere an Eye”
(The GOD Emerging, pp. 183-184)
Alongside such theophany, this time appears your messenger—a most noble servant, and, by the sounds of his final station near Your Innermost, well-rewarded: Dante, now a seraph (“one who burns”) before the highest divine Fire. Nor could You have appointed a more apt figure to lead your newest seer through the layers of the Universe! Oh, glory! Glory to the Most High God, He who sits enthroned as the Omega, toward which all things turn. Amen.
– Anonymous

EXPLANATORY ANALYSIS
Reports of seeing highly symmetrical, geometric hallucinations in altered states of consciousness (e.g., while on psychedelics, in deep meditation, etc.) are extremely common, and are well-attested in the literature. Indeed, given the regularity of such experiences, combined with their usual emotional intensity, it is not surprising that many subjects tend to attribute some kind of ontological reality to them—believing them to be some actual, extra-dimensional phenomena, which they are able to access by means of their unique state of awareness.
Of course, the truth of the matter is that, well, no; it really is “all in your head.” The origin of such visual phenomena is to be found in the unique architecture of the visual cortex itself. That is, one is not seeing something “out there,” but actually the mechanics of seeing itself. Or, another way to put it might be this: If you take a photograph of the sun, chances are it will appear as a bright hexagon. Has your camera captured the true nature and shape of our star, otherwise occluded by its intense brightness? No, it’s simply because the lens aperture in your camera is a hexagon that it appears that way. Your image is not telling you anything about the sun, only about your camera.(1) So is it with such geometric hallucinations. They do not correspond to objective entities “out there,” but are rather artefacts of the way your brain processes visual information from your eyes.
The science on such phenomena began to amass in the early twentieth century. In the late 1920s, Heinrich Klüver found through empirical study that the geometric visuals of psychedelics fell into four categories: (1) tunnels and funnels, (2) spirals, (3) lattices, including honeycombs and triangles, and (4) cobwebs. These he called “form constants.”

The Form Constants. Source: Wikipedia.
The regularity of these patterns suggested a source within the human brain itself. Since then, Ermentrout and Cowan (1979) and Bressloff et al. (2002) have provided detailed explanations of Klüver’s form constants. Bresslof et al. offer this anatomical-mathematical basis, writing:
It is well established that the central region of the visual field has a much bigger representation in [the vertical cortex, (henceforth “V1,”] than does the peripheral field (Drasdo, 1977; Sereno et al., 1995). Such a nonuniform retino-cortical magnification is generated by the nonuniform packing density of ganglion cells in the retina, whose axons in the optic nerve target neurons in the lateral geniculate nucleus (LGN), and (subsequently) in V1, that are much more uniformly packed. Let rR = {rR, θR} be the (polar) coordinates of a point in the visual field and r = {x, y} its corresponding V1 coordinates. Given a retinal ganglion cell packing density ρR (cells per unit retinal area) approximated by the inverse square law,

(Drasdo, 1977), and a uniform V1 packing density ρ, we derive a coordinate transformation (Cowan, 1977) that reduces, sufficiently far away from the fovea (when rR » w0/∈) to a scaled version of the complex logarithm (Schwartz, 1977),
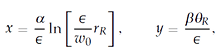
where w0 and ∈ are constants. Estimates of w0 = 0.087 and ∈ = 0.051 in appropriate units can be obtained from Drasdo’s data on the human retina, and a and b are constants. These values correspond to a magnification factor of 11.5 mm/degrees of visual angle at the fovea and 5.75 mm/degrees of visual angle at rR = w0/∈ = 1.7 degrees of visual angle. We can also compute how the complex logarithm maps local edges or contours in the visual field, that is, its tangent map. Let φR be the orientation preference of a neuron in V1 whose receptive field is centered at the point rR in the visual field, and let {r, φ} be the V1 image of {rR, φR}. It can be shown (Wiener, 1994; Cowan, 1997; Bressloff, Cowan, Golubitsky, Thomas, & Wiener, 2001) that under the tangent map of the complex logarithm, φ = φR – θR. Given the retino-cortical map {rR, φR} → {r, φ}, we can compute the form of logarithmic spirals, circles, and rays and their local tangents in V1 coordinates. The equation for spirals can be written as θR = a ln[rR exp(–b)] + c, whence y – c = a(x – b) under the action rR – r. Thus, logarithmic spirals become oblique lines of constant slope a in V1. Circles and rays correspond to vertical (a = ∞) and horizontal (a = 0) lines.
In short, this means that there is a topographic mapping from retinal coordinates to cortical coordinates, as Rule, Stoffregen, and Ermentrout (2011) explain: “That is, a point (r,θ) in polar coordinates on the retina is mapped to (log r,θ) in Cartesian coordinates in the cortex. This means that, for example, the target in figure 1C perceived on the retina is mapped to a series of vertical stripes in the cortex.”

Source: Figure 1 from Rule, Stoffregen, and Ermentrout (2011)
When the uniform state of the visual cortex loses stability, patterns called "planforms" appear, the stable subset of which consist of the following:

Source: Figure 5 from Bressloff et al. (2002)
Combined with the retinal-cortical logarithmic mapping mentioned above, this results in the following patterns—patterns, you'll note, that directly correspond to Klüver’s form constants:

Source: Figure 6 from Bressloff et al. (2002)
Such mapping helps explain the regular frequency of the form constants, such as spirals and mandalas, in hallucinogenic experiences.
Beyond Euclidean geometry, however (which the work of Bressloff et al. assumes for the visual cortex), the importance of non-Euclidean hyperbolic geometry to the DMT experience specifically has been argued by some researchers. Indeed, though Julian does not specify the substance consumed, the experience of a mandalic “flower” and the interaction with mysterious beings may have links to the “Chrysanthemum” and “entity” experiences attested of DMT trips. A “heady chemical hallucination” indeed!
REFERENCES
Bressloff PC, et al. (2002) “What Geometric Visual Hallucinations Tell Us about the Visual Cortex.” Neural Computation 14(3):473-491.
Ermentrout GB, Cowan JD (1979) “A Mathematical Theory of Visual Hallucination Patterns.” Biological Cybernetics 34:137–150.
Rose M, Stoffregen M, Ermentrout B (2011) “A Model for the Origin and Properties of Flicker-Induced Geometric Phosphenes.” PLoS Computational Biology 7(9):e1002158.

FOOTNOTES
(1) This is true of more than Dr. Demonstrand seems to realize, including his own "explanation." Put down the camera and you are still looking through a lens. Does Dr. Demonstrand really believe his math to be any less constructed than an aperture? At least Julian's experience was visceral and embodied. Why should an appeal to lifeless abstractions strike us as more "real"? More real to mathematicians, at least...
– a. verte
V I E W S



